logika matematika melibatkan konsep-konsep seperti proposisi, operator logika, dan penerapannya dalam pemecahan masalah. Di bawah ini adalah beberapa konsep dasar dalam logika matematika:
Proposisi: Proposisi adalah pernyataan yang dapat benar atau salah. Contoh proposisi:
"2 + 2 = 4" (benar)
"Hari ini hujan" (tergantung pada kondisi cuaca)
Operator Logika:
Negasi (¬): Mengubah nilai kebenaran proposisi (misalnya, ¬A berarti "bukan A").
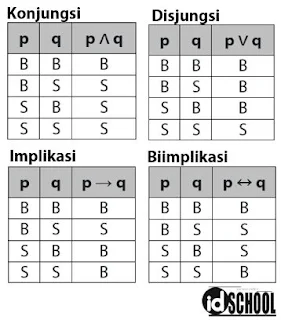
Konjungsi (∧): Menggabungkan dua proposisi, menghasilkan benar hanya jika keduanya benar (misalnya, A ∧ B benar jika A dan B benar).
Disjungsi (∨): Menggabungkan dua proposisi, menghasilkan benar jika salah satu atau keduanya benar (misalnya, A ∨ B benar jika A atau B benar).
Implikasi (→): Menghubungkan dua proposisi, menghasilkan benar kecuali jika premis benar dan kesimpulan salah (misalnya, A → B benar jika A benar dan B benar, atau jika A salah).
Bikonduksi (↔): Menghubungkan dua proposisi, menghasilkan benar jika keduanya memiliki nilai kebenaran yang sama (misalnya, A ↔ B benar jika A dan B memiliki nilai kebenaran yang sama).
Tautologi dan Kontradiksi:
Tautologi: Sebuah proposisi yang selalu benar, tidak peduli nilai kebenaran proposisi komponen (contohnya, A ∨ ¬A selalu benar).
Kontradiksi: Sebuah proposisi yang selalu salah, tidak peduli nilai kebenaran proposisi komponen (contohnya, A ∧ ¬A selalu salah).
Hukum Logika:
Hukum Idempoten: A ∧ A = A, A ∨ A = A.
Hukum Komutatif: A ∧ B = B ∧ A, A ∨ B = B ∨ A.
Hukum Asosiatif: (A ∧ B) ∧ C = A ∧ (B ∧ C), (A ∨ B) ∨ C = A ∨ (B ∨ C).
Hukum Distributif: A ∧ (B ∨ C) = (A ∧ B) ∨ (A ∧ C), A ∨ (B ∧ C) = (A ∨ B) ∧ (A ∨ C).
Ini hanya gambaran singkat tentang logika matematika. Terdapat konsep-konsep yang lebih lanjut seperti tabel kebenaran, bentuk normal, dan penerapan dalam pemrograman dan pemecahan masalah lainnya. Jika Anda memiliki pertanyaan lebih spesifik tentang konsep tertentu atau penerapannya, silakan beri tahu saya!