Menerapkan strategi algoritmik standar untuk menghasilkan beberapa solusi persoalan dengan data diskrit bervolume tidak kecil pada kehidupan sehari-hari maupun menerapkan dalam program komputer.
Tahukah Anda, seringkali kita melihat beberapa kalimat digabung menjadi satu kalimat yang lebih panjang. Misalnya, kalimat "100 adalah bilangan genap dan 99 adalah bilangan ganjil" merupakan gabungan dari dua kalimat, yaitu "100 adalah bilangan genap" dan "99 adalah bilangan ganjil". Dalam logika, terdapat lima jenis penghubung yang dikenal, yaitu negasi/ingkaran, konjungsi, disjungsi, dan implikasi.
Negasi atau ingkaran suatu pernyataan adalah suatu pernyataan yang bernilai benar (B), jika pernyataan semula bernilai salah (S), dan sebaliknya. Ketika sebuah kalimat pernyataan bernilai benar, setelah dinegasikan, kalimat itu akan menjadi salah. Sebaliknya, jika sebuah kalimat pernyataan bernilai salah, setelah dinegasikan, kalimat tersebut akan menjadi benar.
Contoh kalimat negasi (ingkaran):
Ikan hanya bisa hidup di air. (benar)
Negasinya: Ikan bisa hidup di darat. (salah)
Monyet pandai memanjat pohon. (benar)
Negasinya: Monyet pandai menanam pohon. (salah)
Konjungsi
Kata hubung konjungsi adalah “dan” dengan simbol “˄”. Sehingga semua pernyataan majemuk yang dibentuk oleh kata penghubung “dan” disebut konjungsi.
Misalkan tersedia data sebagai berikut.
p : Tahun 2004 adalah tahun kabisat (habis dibagi 4).
q : Bulan Februari di tahun 2020 memiliki 29 hari.
Apabila pernyataan di atas dinegasikan, maka akan terbentuk kalimat sebagai berikut.
~p : Tahun 2024 bukan tahun kabisat.
~q : Bulan Februari di tahun 2020 memiliki 28 hari.
Dari pernyataan di atas, dapat disusun kalimat konjungsi sebagai berikut.
1. Tahun 2020 adalah tahun kabisat dan memiliki 29 hari di bulan Februari.
Bernilai benar
2. Tahun 2020 adalah tahun kabisat dan memiliki 28 hari di bulan Februari.
Bernilai salah
3. Tahun 2020 bukan tahun kabisat dan memiliki 29 hari di bulan Februari.
Bernilai salah
4. Tahun 2020 bukan tahun kabisat dan memiliki 28 hari di bulan Februari.
Bernilai salah
Dari deskripsi di atas, dapat kita susun tabel nilai kebenaran dari konjungsi, yaitu
sebagai berikut.
Perhatikan contoh kalimat konjungsi.
1. Perhatikan pernyataan berikut.
p : Kambing berkaki empat. (benar)
q : Kambing memiliki sayap. (salah)
Tentukan kalimat konjungsi dan nilai kebenarannya!
p ˄ q : Kambing berkaki empat dan memiliki sayap. (salah)
2. Kalimat “Presiden adalah pimpinan tertinggi dan berasal dari rakyat”.
Kalimat di atas bernilai benar, alasannya adalah …
p : Presiden adalah pimpinan tertinggi. (benar)
q : Presiden berasal dari rakyat. (benar)
Dikarenakan keduanya bernilai benar, maka dipastikan kalimat di atas bernilai benar.
3. Disjungsi
Dua kalimat deklaratif yang dihubungkan dengan kata hubung “atau” dan ditulis “˅”
disebut disjungsi. Untuk menentukan tabel kebenaran dari disjungsi, lakukan cara yang
sama seperti membuat tabel kebenaran konjungsi.
Misalkan tersedia data sebagai berikut:
p : Tahun 2000 adalah tahun kabisat (habis dibagi 4).
q : Bulan Februari di tahun 2020 memiliki 29 hari.
Apabila pernyataan diatas dinegasikan, maka akan terbentuk kalimat sebagai berikut.
~p : Tahun 2020 bukan tahun kabisat.
~q : Bulan Februari di tahun 2020 memiliki 28 hari.
Dari pernyataan di atas, dapat dibentuk kalimat disjungsi sebagai berikut.
1. Tahun 2020 adalah tahun kabisat dan memiliki 29 hari di bulan Februari.
Bernilai benar
2. Tahun 2020 adalah tahun kabisat dan memiliki 28 hari di bulan Februari.
Bernilai salah
3. Tahun 2020 bukan tahun kabisat dan memiliki 29 hari di bulan Februari.
Bernilai salah
4. Tahun 2020 bukan tahun kabisat dan memiliki 28 hari di bulan Februari.
Bernilai salah
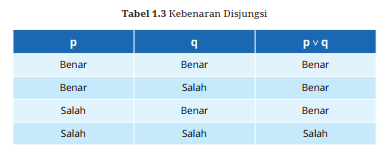
Dari deskripsi di atas, dapat kita susun tabel nilai kebenaran dari disjungsi, yaitu
sebagai berikut
Perhatikan contoh kalimat disjungsi.
1. Perhatikan informasi berikut.
p : 5 * 5 = 25 (benar)
q : 25 adalah bilangan ganjil. (benar)
Tentukan nilai disjungsi dan nilai kebenarannya!
p ˅ q : 5 * 5 = 25 atau 25 adalah bilangan ganjil. (benar)
2. Perhatikan informasi berikut.
p : lumba-lumba adalah hewan mamalia. (benar)
q : lumba-lumba merupakan hewan karnivora. (benar)
p ˅ q : lumba-lumba adalah hewan menyusui atau hewan karnivora. (benar)
Implikasi
Pernyataan majemuk yang dibentuk oleh kata hubung “jika … maka …” disebut implikasi dengan simbol →. Untuk menentukan nilai tabel kebenarannya, perhatikan contoh berikut. Misal, jika Ismah lulus ujian, maka ia akan memberikan uang kepada adiknya.
Misalnya:
P : Ismah lulus ujian.
Q : Ismah memberikan uang kepada adiknya.
Sekarang kita tentukan negasi dari P dan Q sebagai berikut.
~P : Ismah tidak lulus ujian.
~Q : Ismah tidak memberikan uang kepada adiknya.
Dari pernyataan di atas, dapat dibuat hubungan implikasi sebagai berikut.
1. Jika Ismah lulus ujian, maka ia akan memberikan uang kepada adiknya.
(Kalimat ini benar karena Ismah lulus ujian (P: benar) dan memberikan uang kepada adiknya (Q: benar)).
2. Jika Ismah lulus ujian, maka ia tidak memberikan uang kepada adiknya.
(Kalimat ini salah karena Ismah lulus ujian (P: benar) dan tidak memberikan uang kepada adiknya (Q: salah)).
3. Jika Ismah tidak lulus ujian, maka ia memberikan uang kepada adiknya.
(Kalimat ini benar karena Ismah tidak lulus ujian (P: salah) dan memberikan uang kepada adiknya (Q: benar)).
4. Jika Ismah tidak lulus ujian, maka ia tidak memberikan uang kepada adiknya.
(Kalimat ini benar karena Ismah tidak lulus ujian (P: salah) dan memberikan uang kepada adiknya (Q: benar)).
Dari gambaran di atas, kita dapat menyusun nilai tabel kebenaran implikasi sebagai berikut.
Contoh implikasi:
1. Tentukan nilai kebenaran dari implikasi dua pernyataan berikut!
p : Semua orang akan mengalami masa tua.
q : Semua orang akan meninggal dunia.
Jawab
p → q : Jika semua orang mengalami masa tua, maka kelak akan meninggal dunia.
(benar)
2. Tentukan nilai kebenaran dari implikasi dua pernyataan berikut!
p : 14 / 2 = 7 (benar)
q : 7 adalah bilangan ganjil. (benar)
Jawab
p → q : Jika 14 / 2 = 7, maka 7 adalah bilangan ganjil. (benar)
Deduktif, Induktif, dan Abduktif
Penalaran adalah proses berpikir berdasarkan pengamatan indera (observasi empirik) yang menghasilkan sejumlah konsep dan pengertian. Pengamatan sejenis akan membentuk proposisi-proposisi sejenis, berdasarkan sejumlah proposisi yang diketahui atau dianggap benar, kemudian disimpulkan sebuah proposisi baru yang tidak diketahui sebelumnya. Proses ini disebut menalar. Terdapat tiga jenis metode dalam menalar yaitu deduktif, induktif dan abduktif.
1. Deduktif
Penalaran deduktif adalah proses penalaran yang bertujuan untuk menarik kesimpulan berupa prinsip atau sikap khusus berdasarkan fakta-fakta yang bersifat umum. Dengan kata lain deduktif merupakan suatu penalaran untuk menyimpulkan hal khusus dari sejumlah proposisi umum.
Penalaran deduktif adalah kegiatan berpikir yang berbeda bahkan berlawanan dengan penalaran induktif. Deduktif merupakan penalaran atau cara berpikir untuk menyatakan pernyataan yang bersifat khusus dari pernyataan-pernyataan yang bersifat umum. Dijelaskan bahwa untuk menarik kesimpulan secara deduktif diperlukan pola pikir yang disebut silogisme yang tersusun dari dua buah pernyataan (premis) dan sebuah kesimpulan (konklusi).
Perhatikan contoh berikut.
1. Semua manusia akan mati (Premise 1). Paidi adalah manusia (Premise 2). Jadi Paidi akan mati (Konklusi).
2. Beras merupakan komoditas bagi orang Indonesia (umum), tetapi ada beberapa wilayah yang penduduknya mengkonsumsi sagu (khusus) seperti Maluku dan Papua (khusus).
Macam-macam penalaran deduktif, antara lain:
a. Silogisme
Silogisme adalah proses membuat kesimpulan secara deduktif. Silogisme tersusun dari dua proposisi (pernyataan) dan konklusi (kesimpulan). Silogisme dirangkai dari tiga buah pendapat yang terdiri dari 2 pendapat dan 1 kesimpulan.
1) Silogisme Negatif
Setiap kalimat yang di dalamnya terdapat kata “bukan ataupun tidak” pada premis biasanya disebut dengan Silogisme Negatif dan begitu juga simpulan.
Jadi, jika suatu premis pada silogisme bersifat negatif, maka kesimpulannya pun bersifat negatif juga.
Misal:
Premis 1 : Penderita kurang darah tidak boleh makan buah melon.
Premis 2 : Budi menderita penyakit kurang darah.
Konklusi : Budi tidak boleh makan buah melon.
2) Silogisme Error
Diperlukan kecermatan dalam menarik kesimpulan menggunakan penalaran silogisme. Untuk merumuskan premis, diwajibkan mencermati setiap kalimat yang akan dibuat agar tidak menimbulkan kesalahpahaman. Perhatikan contoh silogisme error berikut.
Premis 1 : Yanto lulus ujian SBMPTN.
Premis 2 : Yanto rajin menabung dan tidak sombong.
Konklusi : Orang yang lulus ujian SBMPTN karena rajin menabung dan tidak sombong?
Konklusi di atas adalah salah karena tidak terdapat premis umum (PU).
b. Entimen
Entimen adalah penalaran deduktif secara langsung atau tanpa silogisme premis atau tidak diucapkan karena sudah diketahui.
Misal:
Premis 1 : Penderita kurang darah tidak boleh makan buah melon.
Premis 2 : Budi menderita penyakit kurang darah.
Konklusi : Budi tidak boleh makan buah melon.
Entimen : Budi tidak boleh makan buah melon karena menderita penyakit kurang darah.
2. Induktif
Induktif adalah proses penarikan kesimpulan dari kasus-kasus nyata secara individual (khusus) menjadi kesimpulan yang bersifat umum. Selain itu, Benyamin Molen (2014:
14) menyatakan bahwa induksi adalah suatu penalaran yang berasal dari pernyataanpernyataan yang bersifat khusus atau tunggal, kemudian ditarik kesimpulan yang bersifat umum.
Selanjutnya Surojiyo, dkk. (2008: 60) menyatakan bahwa induksi adalah proses peningkatan dari hal-hal yang bersifat individual kepada hal yang bersifat universal.
Berdasarkan ketiga definisi tersebut, maka dapat ditarik kesimpulan bahwa induktif adalah proses berfikir untuk menyimpulkan suatu kebenaran yang dilakukan berdasarkan pada apa-apa yang bersifat khusus, kemudian ditarik suatu kesimpulan kebenaran yang sifatnya umum/universal.
Adapun contoh bentuk penalaran induktif adalah elang punya mata, lumba-lumba punya mata, kerbau punya mata, maka dapat ditarik kesimpulan bahwa setiap hewan punya mata. Dibutuhkan banyak sampel untuk mempertinggi tingkat ketelitian premis dari penalaran induktif yang diangkat.
3. Abduktif
Menurut Donny Gahral Adian dan Herdito (Kencana, 2013) menyatakan bahwa abduksi adalah metode untuk memilih argumentasi terbaik dari sekian banyak argumentasi yang mungkin. Oleh sebab itu, abduksi sering disebut dengan argumentasi menuju penjelasan terbaik.
Ada empat cara mendapatkan argumentasi terbaik, yaitu:
a. Kesederhanaan
Jelaskan segala hal dengan bahasa yang ringan dan tidak ada bantahan dari pihak lain.
b. Koherensi
Sebisa mungkin, pilih penjelasan yang sesuai dengan apa yang diyakini para ahli tentang dunia.
c. Prediktabilitas
Sebisa mungkin, pilih penjelasan yang paling banyak menghasilkan prediksi yang dapat disangkal.
d. Komprehensi
Sebisa mungkin pilih penjelasan yang paling lengkap dan meninggalkan sedikit sekali ketidakjelasan.
Adapun contoh dari penalaran abduktif adalah andai kita mengetahui bahwa seseorang yang bernama Gunawan selalu mengendarai mobilnya dengan sangat cepat jika sedang mabuk, maka pada saat kita melihat Gunawan mengendarai mobilnya dengan sangat cepat. Maka kita berkesimpulan bahwa Gunawan sedang mabuk.
Logika Inferensi
Perhatikan kejadian yang ditulis pada kalimat berikut.
Seorang gadis terjatuh ketika berlarian di tengah lapangan karena tersandung batu.
Terlihat muka gadis itu memerah dan kepalanya menunduk. Seorang ibu menghampiri dan segera memeluk gadis tersebut sembari mengatakan tidak apa-apa ayo ke tepi lapangan dan beristirahatlah.
Kalimat di atas dapat disimpulkan bahwa “muka memerah dan kepalanya menunduk” memiliki arti “malu”. Inferensi adalah tindakan/proses untuk mendapatkan kesimpulan berdasarkan apa yang sudah diketahui/diasumsikan.
Pengertian inferensi menurut pendapat para ahli adalah sebagai berikut.
1. Menurut Collins Dictionary, inferensi adalah kesimpulan yang kita tarik tentang sesuatu dengan menggunakan informasi yang sudah kita miliki tentang itu.
2. Menurut Literary Terms, inferensi adalah proses menarik kesimpulan dari bukti pendukung yang ada. Kita dapat membuat kesimpulan ketika membaca literatur.
Petunjuk diberikan oleh penulis tentang apa yang terjadi, dan kita harus mencari tahu berdasarkan bukti itu. Penulis menyiratkan dan para pembaca menyimpulkan.
3. MenurutPhilosophy Terms, inferensi adalah proses menarik kesimpulan berdasarkan bukti yang ada. Berdasarkan beberapa bukti atau “premis”, kita membuat sebuah kesimpulan.
4. Menurut Your Dictionary, istilah inferensi mengacu pada proses observasi atau pengamatan dan pengetahuan untuk menentukan kesimpulan yang masuk akal.
1. Jenis Inferensi
Dilihat berdasarkan jumlah premisnya, inferensi pada dasarnya diklasifikasikan menjadi dua:
a. Inferensi langsung (immediate inference), yaitu proses membuat kesimpulan dari sebuah premis.
b. Inferensi mediasi (mediate inference), proses membuat kesimpulan/konklusi dari dua atau lebih premis yang saling terkait secara logis.
2. Contoh Logika Inferensi
a. Ismah pulang ke rumah pada pukul 14.00, terlihat pintu rumah masih terkunci karena ayahnya pulang kerja pukul 15.00.
Ismah melihat tidak ada alas kaki di teras rumahnya sehingga menyimpulkan bahwa ayahnya belum pulang.
b. Luluk melihat asap mengepul dari ruang dapur dan mencium bau gosong.
Luluk menyimpulkan bahwa ada yang terbakar di ruang dapur.
c. Budi melihat banyak semut mengerumuni remahan roti di bawah meja.
Budi menyimpulkan bahwa anaknya lupa membersihkan sisa makanan
d. Bambang bekerja sebagai guru dan setiap pulang kerja merenovasi rumahnya tanpa bantuan tukang bangunan.
Dapat disimpulkan bahwa selain sebagai guru, Bambang memiliki keahlian sebagai tukang bangunan.